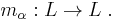Field norm
In mathematics, the (field) norm is a mapping defined in field theory, to map elements of a larger field into a smaller one.
Contents |
Formal definitions
1. Let K be a field and L a finite extension (and hence an algebraic extension) of K. Multiplication by α, an element of L, is a K-linear transformation
That is, L is viewed as a vector space over K, and mα is a linear transformation of this vector space into itself. The norm NL/K(α) is defined as the determinant of this linear transformation. Properties of the determinant imply that the norm belongs to K and
- NL/K(αβ) = NL/K(α)NL/K(β)
so that the norm, when considered on non-zero elements, is a group homomorphism from the multiplicative group of L to that of K.
2. If L/K is a Galois extension, the norm NL/K of an element α of L is the product of all the conjugates
- g(α)
of α, for g in the Galois group G of L/K.
Example
The field norm from the complex numbers to the real numbers sends
- x + iy
to
- x2 + y2. This corresponds to the Galois group having two elements, the identity element which sends x + iy to itself, and complex conjugation, which sends x + iy to x - iy.
Further properties
The norm of an algebraic integer is again an integer, because it is equal (up to sign) to the constant term of the minimal polynomial.
In algebraic number theory one defines also norms for ideals. This is done in such a way that if I is an ideal of OK, the ring of integers of the number field K, N(I) is the number of residue classes in OK/I - i.e. the cardinality of this finite ring. Hence this norm of an ideal is always a positive integer. When I is a principal ideal αOK there is the expected relation between N(I) and the absolute value of the norm to Q of α, for α an algebraic integer.
See also
References
- Roman, Steven (2006), Field theory, Graduate Texts in Mathematics, 158 (Second ed.), Springer, Chapter 8, ISBN 978-0-387-27677-9